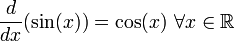Integrantes:
karla Sofía Arias Venegas.
Fatima Anahi Enriquez Aviña.
Hilda Yoshira Loo Gonzalez.
Alejandra Lizbeth Quintanilla Garza.
Joel Eduardo Ruiz Perez.
Maria Guadalupe Velez Ramirez.
jueves, 3 de diciembre de 2015
miércoles, 2 de diciembre de 2015
FORMULAS FUNDAMENTALES DE LA INTEGRACION
| 1.- |
| 2.- |
| 3.- |
| 4.- |
| 5.- |
| 6.- |
| 7.- |
| 8.- |
| 9.- |
| 10.- |
| 11.- |
| 12.- |
| 13.- |
| 14.- |
| 15.- |
| 16.- |
| 17.- |
| 18.- |
| 19.- |
| 20.- |
| 21.- |
| 22.- |
| 23.- |
| 24.- |
25.-
|
26.-
|
27.-
|
28.-
|
VIDEOS DE APOYO SOBRE LAS DIFERENTES SITUACIONES DEL CALCULO INTEGRAL
Lección 1 Introducción al concepto de Antiderivada 1 (Integral Indefinida) .
URL:http://aula.tareasplus.com/…/Introduccion-al-concepto-de-an…
URL:http://aula.tareasplus.com/…/Introduccion-al-concepto-de-an…
Lección 2 Introducción al concepto de Antiderivada 2 (Integral Indefinida).
URL:http://aula.tareasplus.com/…/Introduccion-al-concepto-de-an…
URL:http://aula.tareasplus.com/…/Introduccion-al-concepto-de-an…
Lección 3 Introducción al concepto de Antiderivada 3 (Integral Indefinida) .
URL:http://aula.tareasplus.com/…/Introduccion-al-concepto-de-an…
URL:http://aula.tareasplus.com/…/Introduccion-al-concepto-de-an…
Lección 4 Integral de una función a la n, Parte 1.
URL:http://aula.tareasplus.com/…/Integral-de-una-funcion-a-la-n…
URL:http://aula.tareasplus.com/…/Integral-de-una-funcion-a-la-n…
Lección 5 Integral de una función a la n, Parte 2
URL:http://aula.tareasplus.com/…/Integral-de-una-funcion-a-la-n…
URL:http://aula.tareasplus.com/…/Integral-de-una-funcion-a-la-n…
Lección 6 Integrales que generan logarítmos naturales, Parte 1
URL:http://aula.tareasplus.com/…/Integrales-que-generan-logarit…
URL:http://aula.tareasplus.com/…/Integrales-que-generan-logarit…
Lección 7 Integrales que generan logarítmos naturales, Parte 2
URL:http://aula.tareasplus.com/…/Integrales-que-generan-logarit…
URL:http://aula.tareasplus.com/…/Integrales-que-generan-logarit…
Lección 34 Integral de la función exponencial
URL:http://aula.tareasplus.com/…/Integral-de-la-funcion-exponen…
URL:http://aula.tareasplus.com/…/Integral-de-la-funcion-exponen…
Lección 35 Integral de la función Seno
URL:http://aula.tareasplus.com/…/CA…/Integral-de-la-funcion-seno
URL:http://aula.tareasplus.com/…/CA…/Integral-de-la-funcion-seno
Lección 36 Integral de la función Coseno
URL:http://aula.tareasplus.com/…/…/Integral-de-la-funcion-coseno
URL:http://aula.tareasplus.com/…/…/Integral-de-la-funcion-coseno
Lección 37 Integral de la función Tangente
URL:http://aula.tareasplus.com/…/Integral-de-la-funcion-tangente
URL:http://aula.tareasplus.com/…/Integral-de-la-funcion-tangente
Lección 38 Integral de la función Cotangente
URL:http://aula.tareasplus.com/…/Integral-de-la-funcion-cotange…
URL:http://aula.tareasplus.com/…/Integral-de-la-funcion-cotange…
Lección 39 Integral de las funciones secante y cosecante al cuadrado
URL:http://aula.tareasplus.com/…/Integral-de-las-funciones-seca…
URL:http://aula.tareasplus.com/…/Integral-de-las-funciones-seca…
Lección 40 Integral del producto secante por tangente y cosecante por cotangente
URL:http://aula.tareasplus.com/…/Integral-del-producto-secante-…
URL:http://aula.tareasplus.com/…/Integral-del-producto-secante-…
Lección 41 Integrales de tipo arco o argumento (inversas trigonométricas)
URL:http://aula.tareasplus.com/…/Integrales-tipo-arco-o-argumen…
URL:http://aula.tareasplus.com/…/Integrales-tipo-arco-o-argumen…
Lección 42 Integral de una función secante
URL:http://aula.tareasplus.com/…/CALCULO-INTEGRAL/Integral-de-l…
URL:http://aula.tareasplus.com/…/CALCULO-INTEGRAL/Integral-de-l…
Lección 43 Integral de la función cosecante
URL:http://aula.tareasplus.com/…/Integral-de-la-funcion-cosecan…
URL:http://aula.tareasplus.com/…/Integral-de-la-funcion-cosecan…
Lección 51 Introducción a la Integración por partes
URL:http://aula.tareasplus.com/…/Introduccion-a-la-integracion-…
URL:http://aula.tareasplus.com/…/Introduccion-a-la-integracion-…
Lección 52 LIATE a la integración por partes
URL:http://aula.tareasplus.com/…/LIATE-en-la-integracion-por-pa…
URL:http://aula.tareasplus.com/…/LIATE-en-la-integracion-por-pa…
Lección 53 Integración por partes (Ejemplos parte 1)
URL:http://aula.tareasplus.com/…/Integracion-por-partes-ejemplo…
URL:http://aula.tareasplus.com/…/Integracion-por-partes-ejemplo…
Lección 54 Integración por partes (Ejemplos parte 2)
ORL:http://aula.tareasplus.com/…/Integracion-por-partes-ejemplo…
ORL:http://aula.tareasplus.com/…/Integracion-por-partes-ejemplo…
Lección 55 Integración por partes (Ejemplos parte 3)
URL:http://aula.tareasplus.com/…/Integracion-por-partes-ejemplo…
URL:http://aula.tareasplus.com/…/Integracion-por-partes-ejemplo…
Lección 56 Integral por partes
URL:http://aula.tareasplus.com/…/CALCULO-IN…/Integral-por-Partes
URL:http://aula.tareasplus.com/…/CALCULO-IN…/Integral-por-Partes
Lección 57 Integral por partes 2
URL:http://aula.tareasplus.com/…/CALCULO-…/Integral-por-Partes-2
URL:http://aula.tareasplus.com/…/CALCULO-…/Integral-por-Partes-2
Lección 58 Solución de una integral por partes
URL:http://aula.tareasplus.com/…/Solucion-de-una-Integral-por-P…
URL:http://aula.tareasplus.com/…/Solucion-de-una-Integral-por-P…
Lección 59 Integración recurrente y la integración por partes
URL:http://aula.tareasplus.com/…/Integracion-recurrente-y-la-in…
URL:http://aula.tareasplus.com/…/Integracion-recurrente-y-la-in…
Lección 60 Integrales trigonométricas, Caso 1
URL:http://aula.tareasplus.com/…/Integrales-trigonometricas-cas…
URL:http://aula.tareasplus.com/…/Integrales-trigonometricas-cas…
APLICACION DEL CALCULO INTEGRAL
CALCULO INTEGRAL EN EL ÁREA DE:
- INGENIERA
Aunque no se trata de una herramienta de uso cotidiano del ingeniero, el cálculo integral tiene aplicaciones en el desarrollo de algunos modelos estocásticos para los cuales es indispensable la formulación de integrales. La aplicación de estos modelos va dese la distribución de plantas, hasta la planificación de compras y producción.
INTEGRALES
Ejemplo 1 : La integral sirve para sacar áreas bajo curvas. el odómetro del carro integra la velocidad del carro y obtiene entonces la distancia recorrida x = int(0,t, v dt).
Ejemplo 2 : En el campo de las construcciones , los arquitectos , ingenieros y profesionales de estas áreas usualmente emplean la integral para obtener el área de superficies irregulares.
Ejemplo 3: También la utilizan los administradores cuando trabajan con los costos de una empresa. Al tener el costo marginal de producción de un producto, pueden obtener la formula de costo total a través de integrales.
- MEDICINA
Se plantean y resuelven cosas como la velocidad de propagaciones de una enfermedad, la velocidad de reacción de un medicamento, la taza de crecimiento poblacional de bacterias, la concentración en determinado tiempo de una mezcla que se esta agitando, el enfriamiento que tiene un cadáver y así determinar la hora de fallecimiento.
En la biología; los crecimientos poblacionales, gastos hidráulicos. En óptica son muy usadas las integrales, en bioquímica las determinaciones de los enlaces se hacen por espectros que basan sus áreas bajo las curvas para determinar los enlaces.
También las integrales son usadas para encontrar el angulo de ramificación optimo de vaso sanguíneo para maximizar.
- INFORMÁTICA:
La simulación es una rama de la informática que para emular el comportamiento de un sistema resuelve sistemas de ecuaciones, la forma de resolverlos numéricamente (sin saber la solución matemática) es a través de varios métodos,uno de ellos básicamente calcula integrales en intervalos finitos.
La aplicación del calculo en la ingeniería Informática se ve reflejada en la fabricación chips y placas para distintos uso como son las boards, tarjetas de vídeo, sonido etc. La tecnología en la actualidad tiende a sacar dispositivos cada vez mas pequeños, ese fin se logra gracias al uso del calculo así como la comprensión y edición de audio y vídeo. También es necesario en el uso de surgientes tecnologías como es la artificial y de muchas otras en donde serla base. Ademas también es necesario en la creación de software en el quesea requerido para medición de unidades y simplificación.
INTEGRALES
Integrales:
La integral es la operacion inversa a la diferenciacion.
La integral es la operacion inversa a la diferenciacion.
FORMULAS DE INTEGRACION (INDEFINIDAS)
INTEGRACION INDEFINIDA
Integracion indefinida.
En cálculo infinitesimal, la función primitiva o antiderivada de una función f es una función F cuya derivada es f, es decir,F ′ = f.
Una condición suficiente para que una función f admita primitivas sobre un intervalo es que sea continua en dicho intervalo.
Si una función f admite una primitiva sobre un intervalo, admite una infinidad, que difieren entre sí en una constante: si F1 yF2 son dos primitivas de f, entonces existe un número real C, tal que F1 = F2 + C. A C se le conoce como constante de integración. Como consecuencia, si F es una primitiva de una función f, el conjunto de sus primitivas es F + C. A dicho conjunto se le llama integral indefinida de f y se representa como:
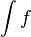 ó
ó 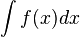
El proceso de hallar la primitiva de una función se conoce como integración indefinida y es por tanto el inverso de la derivación. Las integrales indefinidas están relacionadas con las integrales definidas a través del teorema fundamental del cálculo, y proporcionan un método sencillo de calcular integrales definidas de numerosas funciones.
EJEMPLO:
Una primitiva de la función 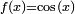 en
en 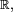 es la función
es la función  ya que:
ya que:
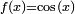 en
en 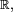 es la función
es la función  ya que:
ya que:
Dado que la derivada de una constante es cero, tendremos que cos(x) tendrá un número infinito de primitivas tales como sin(x), sin(x) + 5, sin(x) - 100, etc. Es más, cualquier primitiva de la función f(x) = cos(x) será de la forma sin(x) + C donde C es una constante conocida como constante de integración.

ANTIDERIVADA
ANTI DERIVADA
La anti derivada es la función que resulta del proceso inverso de la derivación, es decir, consiste en encontrar una función que, al ser derivada produce la función dada.
La anti derivada también se conoce como la primitiva o la integral indefinida se expresa de la siguiente manera: en donde: f(x) es el integrando; dx, la variable de integración o diferencial de x y C es la constante de integración.
Por ejemplo:
Si f(x) = 3×2, entonces, F(x) = x3, es una antiderivada de f(x). Observe que no existe una derivada única para cada función. Por ejemplo, si G(x) = x3+ 5, entonces es otra antiderivada de f(x).
Si f(x) = 3×2, entonces, F(x) = x3, es una antiderivada de f(x). Observe que no existe una derivada única para cada función. Por ejemplo, si G(x) = x3+ 5, entonces es otra antiderivada de f(x).
CLASIFICACION DE LOS NUMEROS
Números naturales
Con los números naturales contamos los elementos de un conjunto (número cardinal). O bien expresamos la posición u orden que ocupa un elemento en un conjunto (ordinal).
El conjunto de los números naturales está formado por:
N= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9,...}
Números enteros
Los números enteros son del tipo:
Nos permiten expresar: el dinero adeudado, la temperatura bajo cero, las profundidades con respecto al nivel del mar, etc.
Números racionales
Se llama número racional a todo número que puede representarse como el cociente de dos enteros, con denominador distinto de cero.
Los números decimales (decimal exacto, periódico puro y periódico mixto) son números racionales; pero los números decimales ilimitados no.
Números racionales(I)
e = 2.718281828459...
Números reales
El conjunto formado por los números racionales e irracionales es el conjunto de losnúmeros reales, se designa por  .
.
Suscribirse a:
Comentarios (Atom)